Stroke and Distance, Part One

If the worst feeling in golf is a shank, the second worst feeling in golf is a shot out of bounds.¹ The stroke and distance penalty for OB or a lost ball leaves you right back where you started – needing to hit the same shot, but now with a score two strokes higher.

I grew up playing junior golf in northwest Wisconsin, where narrow fairways cut through dense forest and the odds of losing a ball in the woods are high. Even while learning to play conservatively off the tee, I would still hit plenty of errant shots out of play. As I stood on the tee after a lost ball or OB I would wonder, “Should I hit the same club that just led to the stroke and distance penalty, or should I play even more conservatively to avoid being back on the tee?”

This is a conundrum many golfers face, and it is useful to have some mathematical rigor to cut through the emotion of a mishit. It turns out this question has a simple answer and a more complicated answer. I will cover the more complicated answer in my next post, but here I will defend the simple answer:

If you made the correct calculation of risk and reward for the first shot, you should keep hitting the same club no matter how many times you go out of bounds.

There is a lot to break down in this statement, so read on to learn exactly how to decide when the risk of OB is worth the reward.

Why you should hit the same club

It may be psychologically challenging to choose to rehit a shot that cost you two strokes and left you back on the tee, but I hope to convince you that this is the right play through a simple argument. To simplify the situation, let’s assume you are deciding between hitting a driver or hitting a hybrid club. Let’s also assume that you have done a careful analysis of your skills and the hole’s defenses (including the OB) and you have determined that with the driver your score on average will be 4.2, while with the hybrid your score will be 4.7 (we will get into how to make this calculation below). Based on these results, you choose to hit the driver because it saves you an average of half a stroke.

Once the drive goes out of bounds, you are back on the tee having taken 2 strokes. Your goal is still to determine how to get from the tee to the hole in as few shots as possible. Your estimations for your expected scores with the driver and the hybrid have not changed, so with the driver you would expect to finish the hole with a score of 6.2, while with the hybrid your expected score is 6.7. Therefore, even though you had bad luck with the driver the first time, it is still the correct choice for your second tee shot.

The big caveat in the above analysis is assuming you have correctly estimated your expected scores with each club. If this was done well, then you have already considered the possibility of going out of bounds with the driver and determined that overall the gain was worth the risk. Remember that one drive is a very small sample size, and as we discussed in a previous post, a single bad shot is not enough evidence to abandon the game plan.²

However, in reality most of our probability calculations are estimates, and even data we have on driving accuracy may be limited. Therefore, while one data point is not enough on its own to change the strategy, it could reveal a miscalculation in our odds. For instance, maybe your ball took a hard bounce off a hill and went out of bounds (like at the Open at Carnoustie this year). If you didn’t account for that possibility in your initial calculation, the expected score with the driver may be too low. In my next post I will get into a method for accounting for this uncertainty. For now, let us assume that we are fairly confident of the chances of going out of bounds.

Calculating Expected Score

Calculating expected score can be a bit challenging without a lot of data, but the overall idea is to estimate the average number of strokes it will take to finish the hole given where you are likely to be after your first shot, second shot, etc.

Let’s use Jordan Spieth’s stats as an example. Suppose Jordan is playing a 420 yard par 4 with a 3 iron off the tee. He hits his 3 iron around 250-260 yards, which would leave him around 160-170 yards to the green. In 2018, Jordan was 0.081 strokes under par on average from 150-175 yards, so we can estimate his scoring average with an iron off the tee as $E_{iron} = 3.92$.

Now suppose Spieth plays the same 420 yard hole but with a driver. I will discuss how to account for the possibility of an out-of-bounds shot in the next section, but for now let us compute the expected score assuming he keeps the ball in play. Jordan averages about 300 yards off the tee, giving him around 120 yards remaining. From 100-125 yards Jordan averaged .189 strokes under par last year, so with a successful drive (in bounds) Jordan’s expected score is $E_{driver}^{(s)} = 3.81$.

This analysis has a number of simplifications (in particular, we ignore the relative likelihood of hitting the fairway or the rough with each club), but neglecting those details for now we see that Jordan will do better on average with a driver off the tee, as one might expect. I will define a new statistic, the Ideal Strokes Gained (ISG), as the number of strokes gained on average when successfully hitting a driver compared to hitting an iron off the tee. In our example with Speith:

\[ ISG = E_{iron}-E_{driver}^{(s)} = 0.11 \]

If Spieth succeeds at keeping his driver in play, he can expect to perform 0.11 strokes better on average than if he hits his iron off the tee. However, this has not accounted for the possibility of a drive out of bounds. The next section will examine when the risk of going out of bounds is worth the Ideal Strokes Gained from a successful drive.

Expected Scores Accounting for OB

At this point, we have computed the expected score with the conservative iron off the tee, $E_{iron}$ and with an aggressive drive that stays in play, $E_{driver}^{(s)}$. We have also argued that the if the driver is worth the risk on shot one, it is still worth the risk on shots 3, 5, 7… (after each OB). We are now in a position to compute the true expected score with the driver accounting for the possibility of one or more shots going out of bounds.

First consider the effects of one drive in play vs out of bounds. Written in words, the equation describing this is:

\[ (\text{Total Expected Score}) = (\text{Prob. in bounds})\times(\text{Score when in bounds})+(\text{Prob. hitting OB})(\text{Score with a shot OB}) \]

Let’s call the probability of keeping the ball in bounds $p$, so the probability of an OB shot is $(1-p)$. The expected score when the tee shot is successfully in bounds is $E_{driver}^{(s)}$, computed in the previous section. For now let’s call $E_{driver}^{(f)}$ the expected score when the first shot fails to stay in bounds. Using these symbols, the word equation above becomes,

\[ E_{driver} = p E_{driver}^{(s)} + (1-p) E_{driver}^{(f)} \]

What about the expected score when the ball is hit out of bounds? Well, the player has already taken 2 strokes (the tee shot itself and the penalty stroke). He is back on the tee hitting a driver again, with the same possible outcomes: a drive in play or another drive OB. Therefore the expected score after one shot out of bounds is:

\[ (\text{Score with a shot OB}) = 2 + (\text{Prob. in bounds})\times(\text{Score when in bounds})+(\text{Prob. hitting OB})(\text{Score with another shot OB}) \]

Written in symbols, this equation is,

\[ E_{driver}^{(f)} = 2+p E_{driver}^{(s)} + (1-p) E_{driver}^{(f)} \]

Notice that $E_{driver}^{(f)}$ appears on both sides of the equation. This should make sense; $E_{driver}^{(f)}$ is the expected score when one drive is out of bounds. If 2 drives are out of bounds, then the expected score is $E_{driver}^{(f)}+2$. With 3 drives OB, the score is $E_{driver}^{(f)}+4$, etc.

We can rearrange the equation above to solve for $E_{driver}^{(f)}$,

\[ E_{driver}^{(f)} = \frac{2}{p} + E_{driver}^{(s)} \]

Using this, we can find the total expected score accounting for all possible out of bounds shots:

\[ E_{driver} = E_{driver}^{(s)}+\frac{2}{p}-2 \]

This equation should make some sense. If the probability of staying in bounds is 1, then all drives will successfully be put in play, and $E_{driver} = E_{driver}^{(s)}$.

If on the other hand, the probability of staying in bounds is very small, then $2/p$ is very large, and the expected score with the driver is very high.

Despite the fact that we do not know for sure how many drives will be out of bounds, the equation above tells us that if we know the probability of going out of bounds and the expected score when the ball is in bounds, we can still compute what the average score with the driver will be.

When to take the risk

By computing the expected score with an iron, $E_{iron}$ and with a driver, $E_{driver}$, it is very straightforward to determine which is the correct strategy. Put simply, the driver is the best choice when $E_{driver}<E_{iron}$. With the equations above, this inequality becomes,

\[ E_{driver}^{(s)}+\frac{2}{p}-2 < E_{iron} \]

or, solving for $p$,

\[ p > \frac{2}{E_{iron}-E_{driver}^{(s)}+2}. \]

We can use the Ideal Strokes Gained statistic defined above to simplify the inequality:

\[ p > \frac{2}{ISG+2}. \]

All of the detail above reduces to a simple equation describing when to take the risk of a stroke-and-distance penalty. Essentially, the threshold at which the risk is worth it depends on the strokes gained with a successful driver over the iron. If the ISG is small, than the probability of staying in bounds has to be very high to make the driver worth it. If there is a big difference in score, however, then the driver is worthwhile even if the probability of success off the tee is lower.

Consider the Jordan Spieth example we used above. Jordan’s ISG for our imaginary hole is 0.11. Using the formula above, he should only hit a driver if he believes his chances of keeping it in play are roughly 95% or better. In other words, if Jordan feels that he will hit more than 1 out of 20 drives out of bounds, then the reward is not worth the risk.

Applying it: OB charts and extensions

The chart below depicts which scenarios are worth the risk of an out-of-bounds shot and which require playing safe:

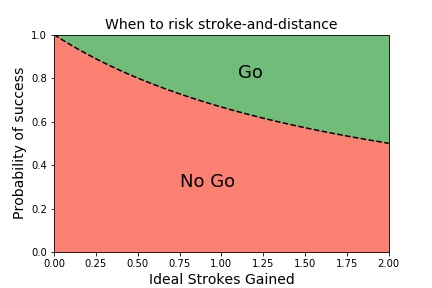
This chart could be used to determine the ideal strategy on a particular shot. If you are faced with the possibility of having to rehit a shot (due to out of bounds, lost ball, or carrying a large hazard), you can determine the correct strategy by taking the following steps:

1. Estimate your average score if you take the conservative approach
2. Estimate your average score if you succeed at taking the risk
3. Compute the difference in these two estimates (ISG)
4. Estimate the probability of having a stroke-and-distance penalty
5. Determine where the probability and ISG are on the chart and act accordingly

This may be too many steps for some, so here are a few shortcut benchmarks you can also consider:

• If success means a full stroke gained, go for it if your chance of putting it in play is 2 in 3.
• If success means a half stroke gained, go for it if your chance of putting it in play is 4 in 5.
• If success means a quarter stroke gained, go for it if your chance of putting it in play is 8 in 9

These three benchmarks can be a quick way to evaluate the riskiness of a strategy that could leave you back on the tee. The bigger the gain, the more it is worth the risk.

As mentioned above, there are a number of challenges to implementing this strategy in the real world. Most notably, the typical golfer will need to estimate all of the parameters involved, which is likely to lead to large amounts of error. Additionally, this calculation only considers the average performance with each strategy. Choosing the risky strategy has a higher chance of both low and high scores, so a player holding a lead will probably play more conservatively than a player who needs to make birdies. Furthermore, as I have discussed previously, A riskier strategy has inherent benefits in terms of wins and money earned, and these benefits may compensate for a slightly higher average score.

The biggest caveat though, is the assumption that we should maintain the same probability $p$ regardless of how many shots go out of bounds. $p$ was, after all, an estimate, and most people would agree that after 3 shots in a row go out of bounds, it seems more likely that our estimate of $p$ was off than that we just ran into bad luck. But how should we account for these shots in a way that doesn’t overreact to new information? Is there a more rigorous way to change course? Stay tuned – I will answer these questions in my next post.